Surviving the Titanic

Paul Hendricks

2017-07-08

Overview

In this vignette, we demonstrate the power of easyml using the popular Titanic dataset.

Load the data

Install the titanic package from CRAN. This package contains datasets providing information on the fate of passengers on the fatal maiden voyage of the ocean liner “Titanic”, with variables such as economic status (class), sex, age and survival. These data sets are often used as an introduction to machine learning on Kaggle. More details about the dataset can be found there.

library(easyml)
## Loaded easyml 0.1.1. Also loading ggplot2.
## Loading required namespace: ggplot2
library(titanic)
library(dplyr)
## 
## Attaching package: 'dplyr'
## The following objects are masked from 'package:stats':
## 
##     filter, lag
## The following objects are masked from 'package:base':
## 
##     intersect, setdiff, setequal, union
library(ggplot2)

data("titanic_train", package = "titanic")
knitr::kable(head(titanic_train))
PassengerId Survived Pclass Name Sex Age SibSp Parch Ticket Fare Cabin Embarked
1 0 3 Braund, Mr. Owen Harris male 22 1 0 A/5 21171 7.2500 S
2 1 1 Cumings, Mrs. John Bradley (Florence Briggs Thayer) female 38 1 0 PC 17599 71.2833 C85 C
3 1 3 Heikkinen, Miss. Laina female 26 0 0 STON/O2. 3101282 7.9250 S
4 1 1 Futrelle, Mrs. Jacques Heath (Lily May Peel) female 35 1 0 113803 53.1000 C123 S
5 0 3 Allen, Mr. William Henry male 35 0 0 373450 8.0500 S
6 0 3 Moran, Mr. James male NA 0 0 330877 8.4583 Q

Tidy the data

To prepare the data for modeling, we will undergo the following steps:

  1. Filter out any places where Embarked is NA,
  2. Add together SibSp, Parch, and 1L to estimate family size,
  3. Create binary variables for each of the 2nd and 3rd class memberships,
  4. Create a binary for gender,
  5. Create binary variables for 2 of the ports of embarkation,
  6. Impute mean values of age where Age is NA.
titanic_train_2 <- titanic_train %>% 
  filter(!is.na(Embarked), Embarked != "") %>% 
  mutate(Family_Size = SibSp + Parch + 1L) %>% 
  mutate(Pclass = as.character(Pclass)) %>% 
  mutate(Pclass_3 = 1 * (Pclass == "3")) %>% 
  mutate(Sex = 1 * (Sex == "male")) %>% 
  mutate(Embarked_Q = 1 * (Embarked == "Q")) %>% 
  mutate(Embarked_S = 1 * (Embarked == "S")) %>% 
  mutate(Age = ifelse(is.na(Age), mean(Age, na.rm = TRUE), Age))

Train a penalized logistic model

To run an easy_glmnet model, we pass in the following parameters:

  • the data set titanic_train_2,
  • the name of the dependent variable e.g. Survived,
  • whether to run a gaussian or a binomial model,
  • how to preprocess the data; in this case, we use preprocess_scale to scale the data,
  • which variables to exclude from the analysis,
  • which variables are categorical variables; these variables are not scaled, if preprocess_scale is used,
  • the random state,
  • whether to display a progress bar,
  • how many cores to run the analysis on in parallel.
.exclude_variables <- c("PassengerId", "Pclass", "Name", 
                        "Ticket", "Cabin", "Embarked")
.categorical_variables <- c("Sex", "SibSp", "Parch", "Family_Size", 
                            "Pclass_3", "Embarked_Q", "Embarked_S")
results <- easy_glmnet(titanic_train_2, "Survived", 
                       family = "binomial", 
                       preprocess = preprocess_scale, 
                       exclude_variables = .exclude_variables, 
                       categorical_variables = .categorical_variables, 
                       random_state = 12345, progress_bar = FALSE, 
                       n_samples = 10, n_divisions = 10, 
                       n_iterations = 2, n_core = 1)

Assess results

Now let’s assess the results of the easy_glmnet model.

Estimates of weights

We can interpret the weights in the following way:

  • A 1 standard deviation increase in Fare increases the log-odds of survival by 0.25 units,
  • For every unit increase in a passenger’s family size, the log-odds of survival decrease by 0.09 units,
  • For every additional Sibling or Spouse in a passenger’s family, the log-odds of survival decrease by 0.17 units,
  • A 1 standard deviation increase in Age decreases the log-odds of survival by 0.37 units,
  • If a passenger embarked at the Southampton port, the log-odds of survival decrease by 0.47 units,
  • If a passenger is third class, the log-odds of survival decrease by 1.44 units,
  • If a passenger is male, the log-odds of survival decrease by 2.53 units.
results$plot_coefficients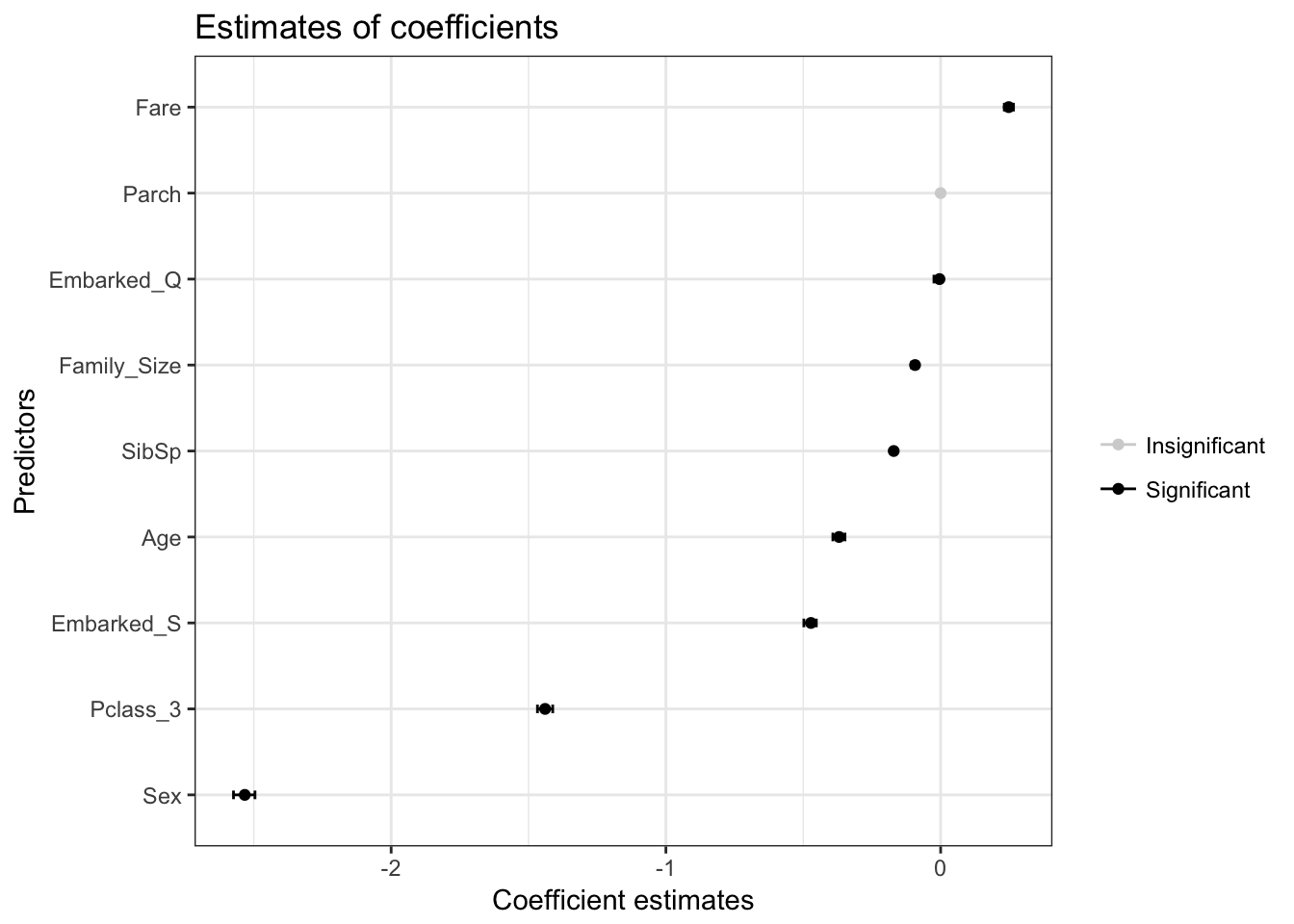

output <- results$coefficients_processed
knitr::kable(arrange(output, desc(mean)), digits  = 2)
predictor mean sd lower_bound upper_bound survival sig dot_color_1 dot_color_2 dot_color
Fare 0.25 0.01 0.23 0.27 1 1 1 2 2
Parch 0.00 0.00 0.00 0.00 0 0 0 1 0
Embarked_Q 0.00 0.01 -0.02 0.00 1 1 1 2 2
Family_Size -0.09 0.01 -0.11 -0.08 1 1 1 2 2
SibSp -0.17 0.01 -0.18 -0.16 1 1 1 2 2
Age -0.37 0.01 -0.39 -0.35 1 1 1 2 2
Embarked_S -0.47 0.01 -0.50 -0.45 1 1 1 2 2
Pclass_3 -1.44 0.02 -1.47 -1.41 1 1 1 2 2
Sex -2.53 0.03 -2.57 -2.50 1 1 1 2 2

Predictions: ROC Curve

We can examine both the in-sample and out-of-sample ROC curve plots for one particular trian-test split determined by the random state and determine the Area Under the Curve (AUC) as a goodness of fit metric. Here, we see that the in-sample AUC is higher than the out-of-sample AUC, but that both metrics indicate the model fits relatively well.

results$plot_predictions_single_train_test_split_train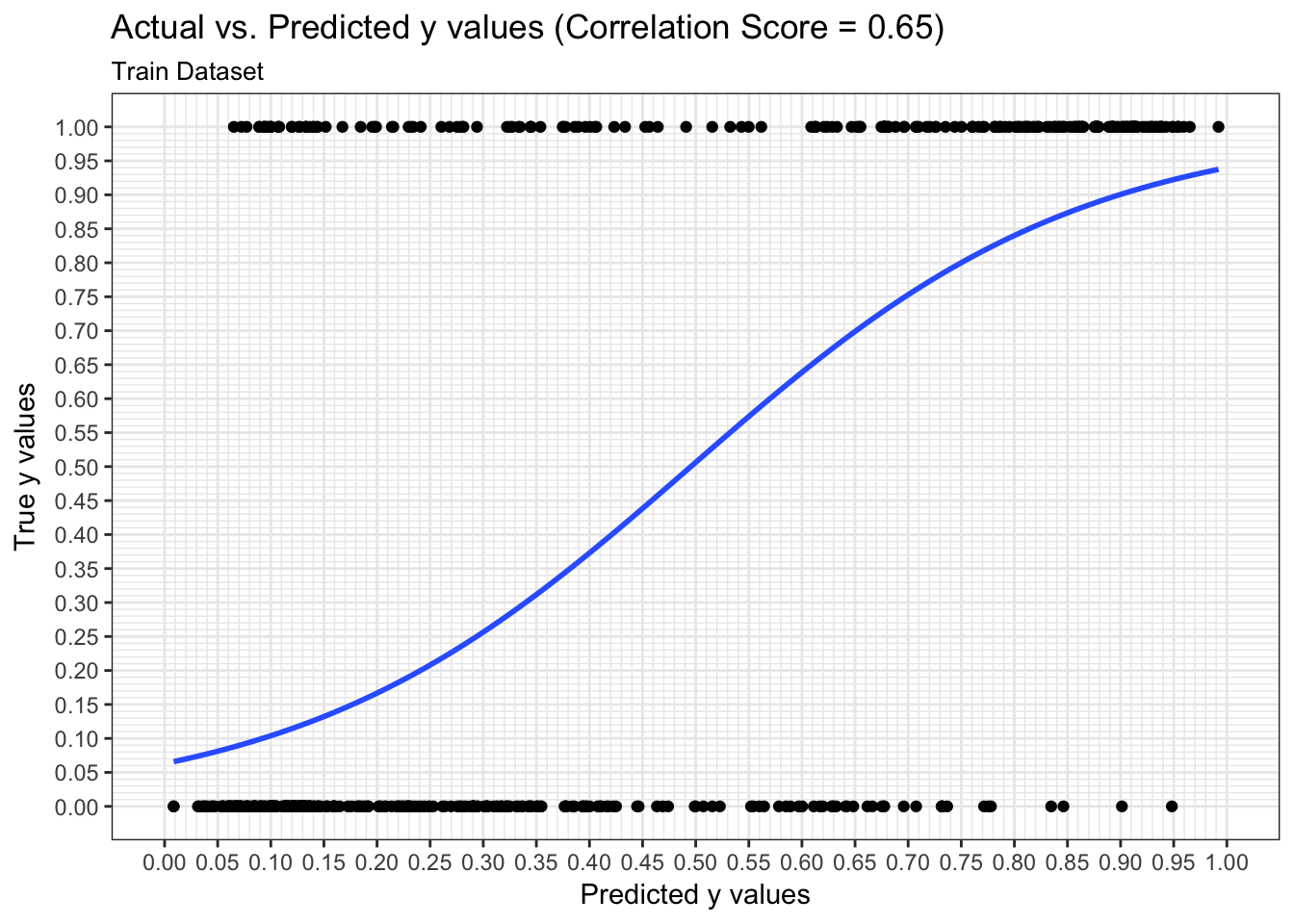

results$plot_predictions_single_train_test_split_test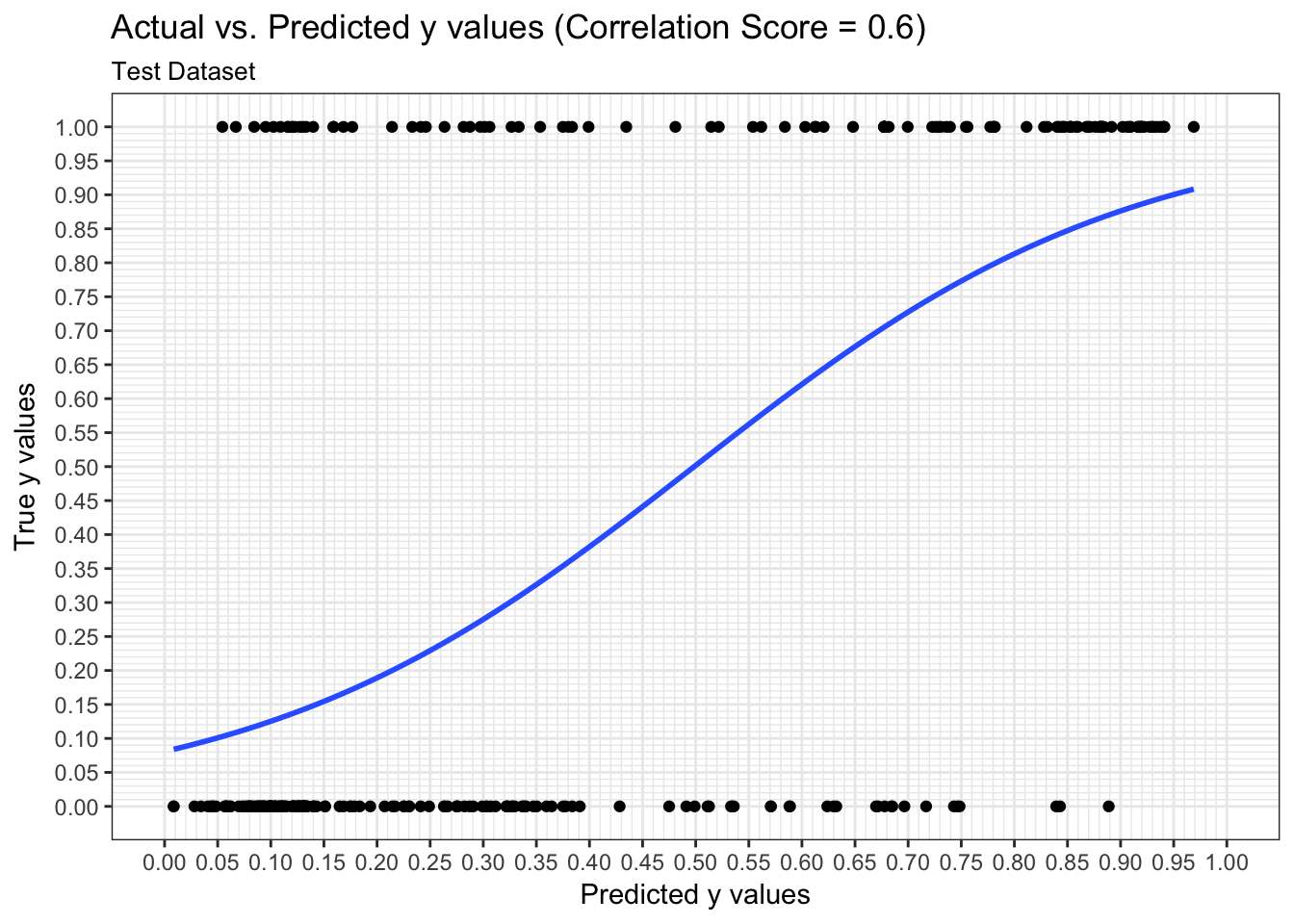

Metrics: AUC

We can examine both the in-sample and out-of-sample AUC metrics for n_divisions train-test splits (ususally defaults to 1,000). Again, we see that the in-sample AUC is higher than the out-of-sample AUC, but that both metrics indicate the model fits relatively well.

results$plot_model_performance_train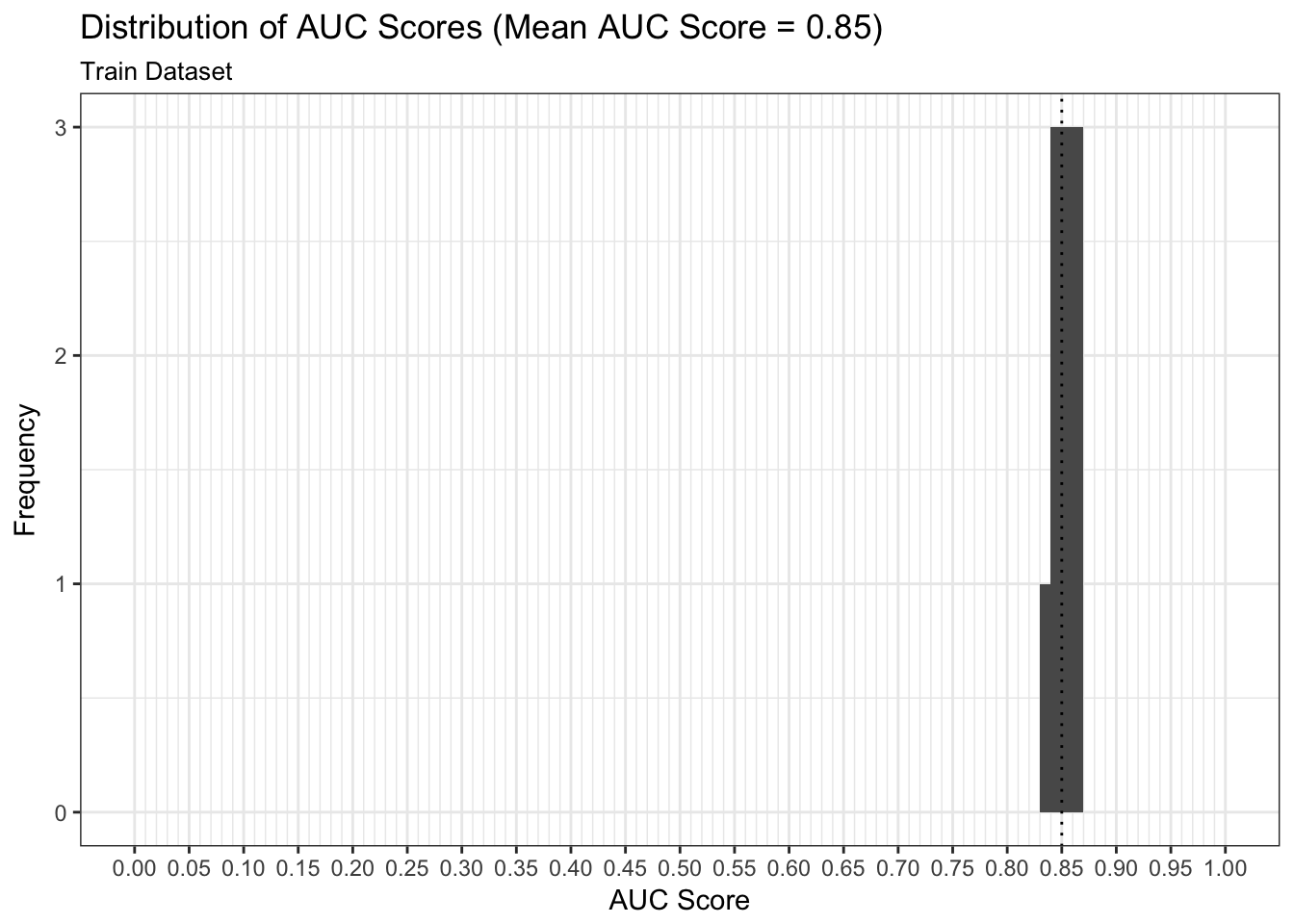

results$plot_model_performance_test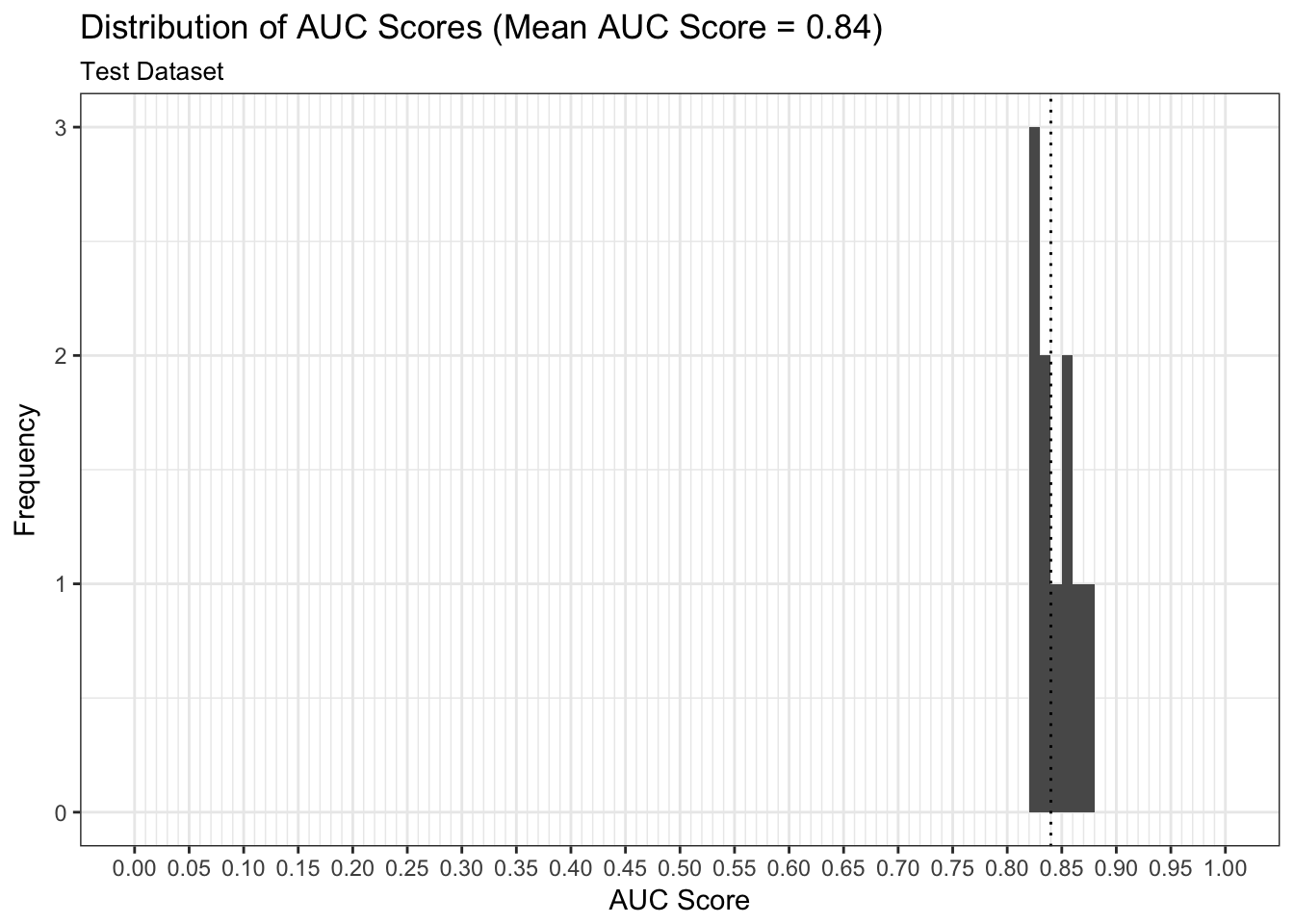

Discuss

In this vignette we used easyml to easily build and evaluate a penalized binomial regression model to assess the likelihood of passenger surival given a number of attributes. We can continue to finetune the model and identify the most optimal alpha/lambda hyperparameter combination; however, our estimates of the weights make intutive sense and a mean out-of-sample AUC of 0.85 right off the bat is indicative of a good model.